-
-
Stress (Pa): Stress is defined as a force acting over an area. This can be modeled by the equation σ=F/A, where F is the load applied (in Newtons) and A (in square meters) is the area it acts upon.
-
Strain: Strain is a unitless measurement of the change in geometry of a given specimen. It is calculated using the equation ε=∆L/L, where ∆L is the change in length and L is the original length. It is often reported in a percentage.
-
-
-
The crosshead moves upward at a fixed rate, applying the load necessary to do so .
-
This load and extension are used by the machine to calculate the stress (σ) and strain (ε), respectively.
-
The stress strain diagram is plotted in real time by the Instron software using this data.
-
-
-
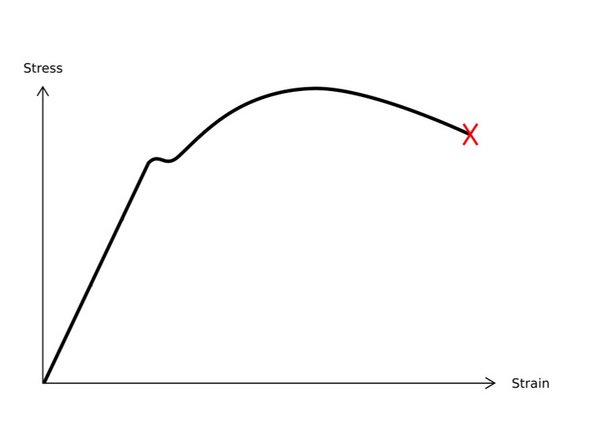
The stress-strain curve is the primary output of the tensile test machine. There are four main material properties that are found in a typical stress-strain curve:
-
Young's Modulus
-
Tensile Yield Strength
-
Ultimate Tensile Strength
-
% Elongation
-
-
-
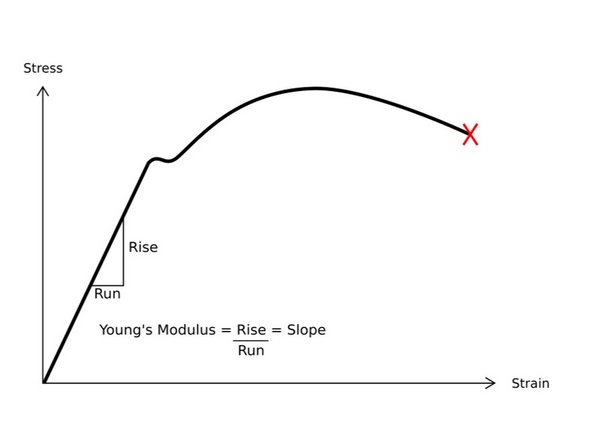
Young's modulus, or the elastic modulus, is the relationship between the stress and strain of a material. In general, it describes the elastic behavior of a material under an externally applied load. Young's Modulus is reported in units of stress (Pascals or psi) over strain (unitless).
-
On the stress-strain curve, Young's modulus is interpreted as the slope of the curve in the elastic region.
-
-
-
The tensile yield strength is the stress at which the material changes from elastic deformation to plastic deformation. A material that exhibits plastic deformation will not return to its original shape upon removal of the applied loads. Tensile yield strength is reported in units of Pascals or psi.
-
Depending on the material, the tensile yield strength may be difficult to identify on the stress-strain curve.
-
Yield Point - On some curves, the tensile yield strength is defined as the point past the elastic region at which the slope is no longer linear and begins to level off.
-
Offset Yield Point - If the yield point cannot be easily identified, the stress at an arbitrary amount of strain (often 0.2%) is defined as the yield strength.
-
-
-
The ultimate tensile strength of a material is the maximum tensile stress it can withstand before failing. Ultimate tensile strength is reported in units of Pascals or psi.
-
On the stress-strain curve, the maximum stress measured is interpreted as the ultimate tensile stress.
-
-
-
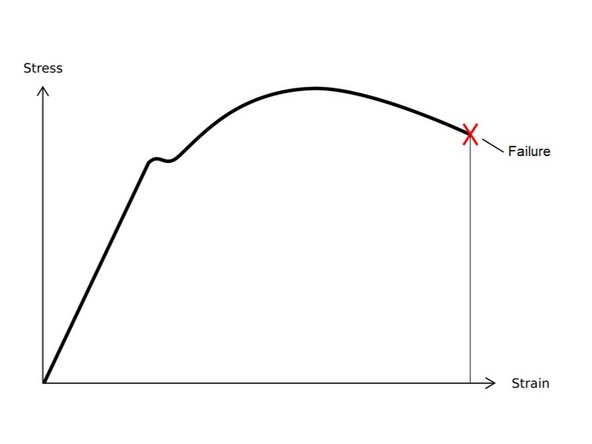
% elongation is defined as the strain of the material at failure. It is reported in %, a dimensionless value.
-
On the stress-strain curve, the strain at failure is defined as the % elongation. In some materials, This value may be found beyond the strain at which the ultimate tensile strength was exhibited.
-
-
-
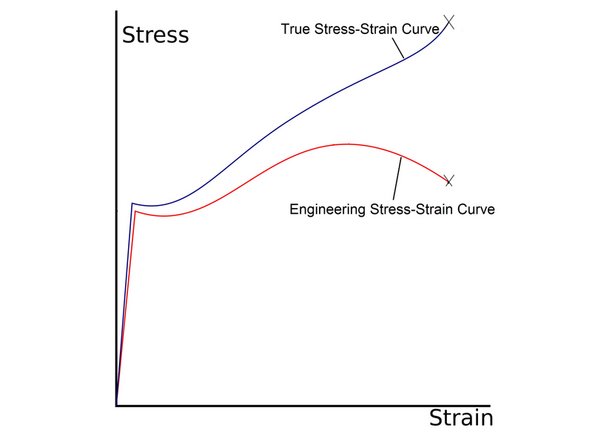
In tensile tests, the tensile force is acting upon the cross sectional area of the sample. The tensile testing machine calculates engineering stress by assuming the cross-sectional area does not change.
-
Realistically, the cross-sectional area changes as the sample deforms and necks. This actual stress is called the true stress.
-
In tensile tests, the original length of the specimen is provided by the operator and the machine calculates the resulting strain as it conducts the test.
-
The tensile testing machine calculates true strain by measuring the the instantaneous gauge length changes as the sample is tested.
-
Almost done!
Finish Line