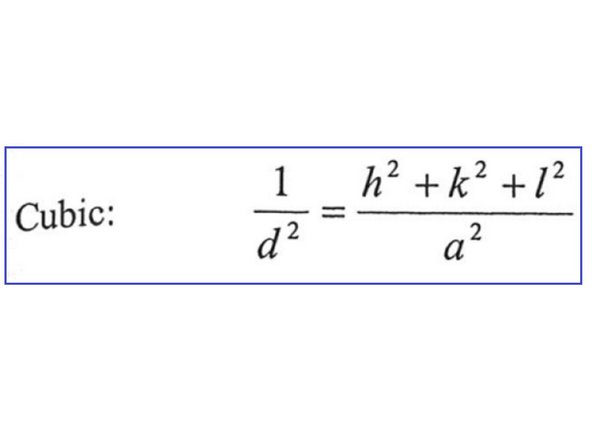-
-
A hot tungsten filament emits electrons.
-
The acceleration potential, 5-40kV, set by the user causes the W photoelectrons to strike the target with 5-40 keV energy.
-
The high energy electrons cause the target, typically Cu, to emit characteristic x-rays; these serve as the x-ray diffraction beam.
-
Water cycles through the system to cool the metal anode target.
-
-
-
The source emits x-rays that can be approximated as plane waves as they encounter the sample.
-
X-rays diffract through the interatomic spacing of the crystal lattice and produce a diffraction pattern of new x-rays.
-
New x-rays interfere and can be assumed to be plane waves when they reach the x--ray detector.
-
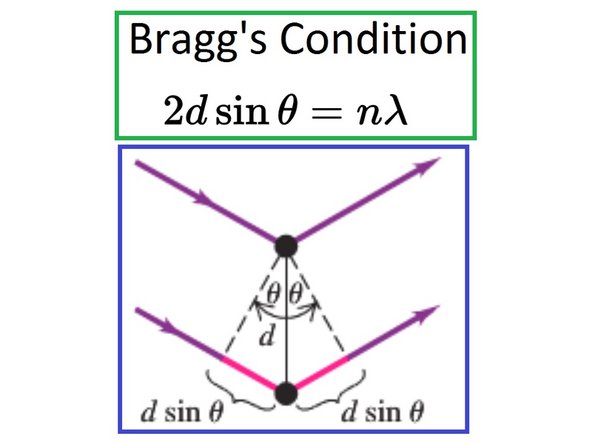
Only x-rays that exhibit constructive interference as described by the Bragg Condition will be detected. All other x-rays waves destructively interfere.
-
This image depicts Laue diffraction, a configuration for transmission diffraction. The diffractometer has a different geometric layout.
-
-
-
The geometry of our system is called "theta/theta" to indicate that the incoming x-ray angle = diffraction angle=theta.
-
This scan mode is "Locked-Coupled" to indicate a locked and coupled positions of the x-ray tube and detector.
-
In theta/theta geometry, only planes parallel to the specimen surface will give rise to x-ray diffraction.
-
-
-
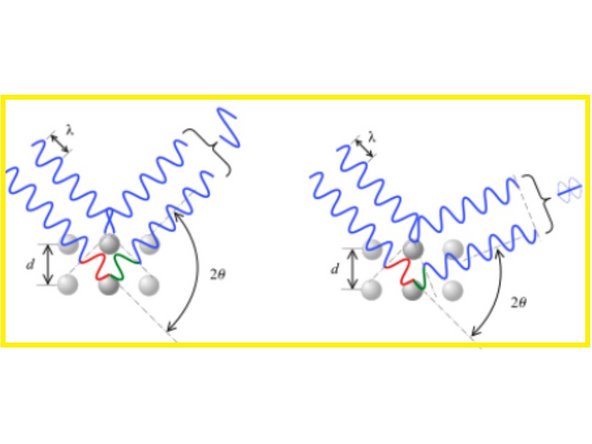
Incident x-rays penetrate the sample and induce scattered x-rays from each electron. The scattered waves that add constructively are also those that meet the Bragg condition. They are called "Reflections."
-
Bragg's condition: n is an integer, d is the interplanar spacing, lambda is the wavelength, theta is the angle between the incident vector and vector normal to the plane.
-
Constructive interference occurs only when the path length difference between parallel planes of atoms is equal to integer multiples of the wavelength of incident x-rays.
-
All other scattered x-rays destructively interfere.
-
-
-
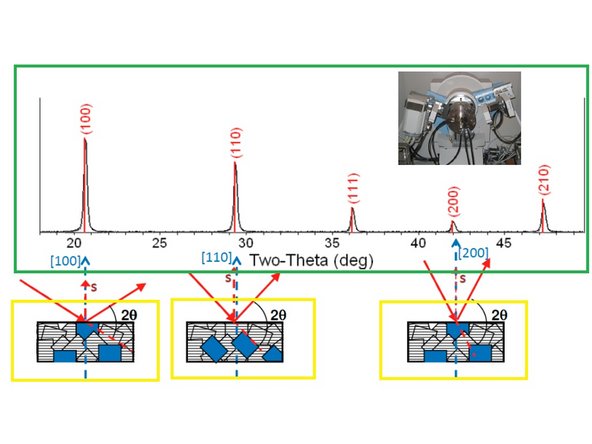
Powder samples ideally have an equal distribution of randomly oriented crystals.
-
Only planes parallel to the surface will diffract in a locked-coupled scan. If your specimen is neither powder nor randomly-oriented, the relative intensities will not match the library patterns.
-
For each peak, only certain orientations of crystal planes will produce constructive interference.
-
Use this formula for cubic lattices to calculate the lattice parameter, peaks, or composition of the sample. h, k, and l refer to the Miller indices of the diffracting plane. a is the lattice parameter.
-
Cancel: I did not complete this guide.
3 other people completed this guide.